НЕЧЕТКИЕ СИСТЕМЫ УПРАВЛЕНИЯ ДИНАМИЧЕСКИМИ ОБЪЕКТАМИ НА ОСНОВЕ МИКРОКОНТРОЛЛЕРОВ.

6.Нечеткие системы управления динамическими объектами на основе микроконтроллеров.

6.1. Принцип организации нечетких систем управления.
6.2. Реализация нечеткого управления.
6.3.Проектирование систем управления динамическими объектами с использованием алгоритмов

6.1. Принцип организации нечетких систем управления.

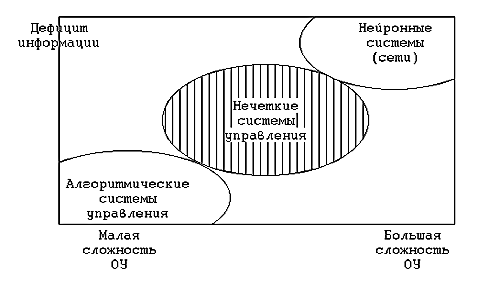
В настоящее время начинают находить широкое применение так называемые нечеткие системы управления (fuzzy-системы), основанные на нечеткой логике, разработанной профессором Лотфи Заде еще в 1965 году [7]. Особенно эффективно применение нечетких систем управления там, где объект управления достаточно сложен для его точного описания и существует дефицит априорной информации о поведении системы. Область применения нечетких систем управления показана на рис. 6.1.

Рис. 6.1. Сфера применения нечетких систем управления.

Принцип действия нечетких систем управления основан на выполнении нечеткого логического вывода типа Нечеткие системы имеют базу знаний и зачатки искусственного интеллекта.

Рис. 6.2. Простейшая одновходовая нечеткая система.

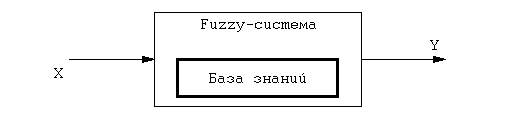
Простейшая система управления, функциональная схема которой показана на рис. 6.2., реализует один восходящий нечеткий вывод, схему которого можно представить в следующем виде

Здесь

- описательная информация - лингвистические переменные, представляемые в виде нечетких множеств

Связь между, например, входной переменной

и соответствующей ей лингвистической переменной

может быть представлена в виде характеристической функции - функции принадлежности, как показано на рис. 6.3. для лингвистической переменной “Высокий”.

Рис. 6.3. Функция принадлежности лингвистической переменной “Высокий”.

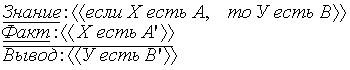
При дискретном представлении функции принадлежности А можно рассматривать как вектор

А=( a₁, a₂,... a_i, ... a_m), 0 ? a_i ? 1.

Аналогично

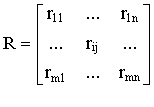B=( b₁, b₂,... b_i, ... b_m), 0 ? b_i ? 1. В нечетком логическом выводе А - причина и В - результат связаны матрицей R, отражающей нечеткие причинно-следственные отношения между А и В. Матрица R может быть представлена в следующем виде

(6.1)

Заде следующим образом определил результат нечеткого восходящего вывода для В’

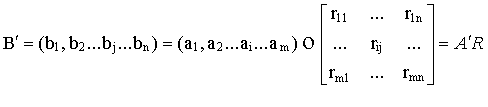(6.2)

Из (6.2) вытекает, что

(6.3)

где - логическое умножение (MIN);
- логическое сложение (MAX).

Для непрерывной логики логическое умножение эквивалентно нахождению минимального значения, а логическое сложение - максимального.

Мамдани предложил следующий вариант нечеткого отношения, наиболее часто используемый на практике

(6.4),

где З- логическое умножение (MIN).

Рассмотрим реализацию нечеткого управления в простейшей системе управления с одним входом и одним нечетким выводом типа на примере системы управления компенсационной емкостью, функциональная схема которой показана на рис. 6.4.

Рис.6.4. Функциональная схема системы управления компенсационной емкостью.

Система должна следить за тем, чтобы в компенсационной емкости К.Е. было достаточное количество жидкости, но не было переполнения.
Система реализует нечеткий вывод типа:
                “Если уровень “высокий”, то открыть” клапан К”.
Таким образом входной лингвистической переменной в данном случае является переменная:
                А = “Высокий”,
а выходной
                В = “Открыть”.
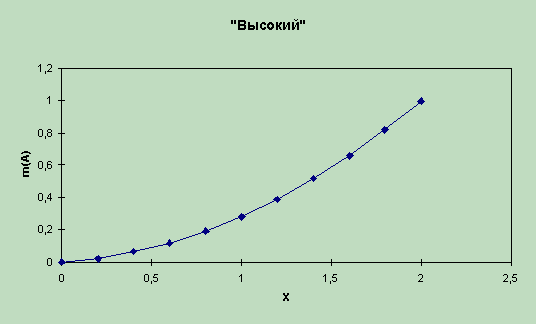
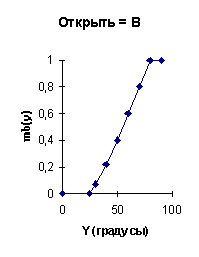
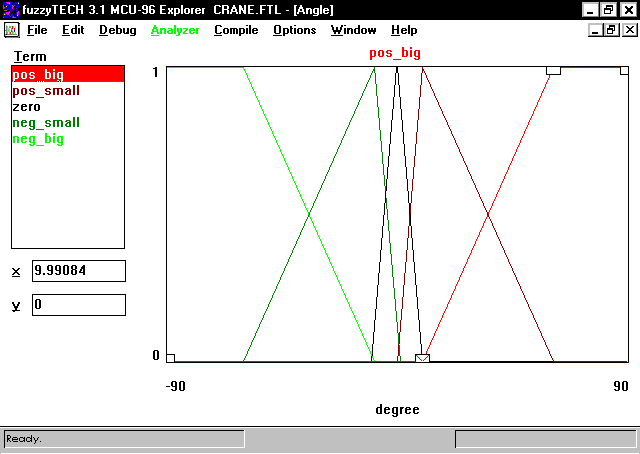
Функции принадлежности, связывающие физическую входную переменную “Уровень” в метрах с лингвистической переменной “Высокий” и выходную переменную “Угол поворота вентиля” с лингвистической переменной “Открыт” показаны соответственно на рис. 6.5, а) и б).

а) б)

Рис. 6.5. Функции принадлежности лингвистических переменных “Высокий” и “Открыть”. В соответствии с приведенными функциями принадлежности входная и выходная лингвистические переменные могут быть представлены в виде следующих дискретных множеств
“Высокий” = m_A(x) = 0.1/1.5 + 0.3/1.6 + 0.7/1.7 + 0.8/1.8 + 0.9/1.9 + 1.0/2.0 + 1.0/2.1 + 1.0/2.2;
“Открыть” = m_B(y) = 0.1/30° + 0.3/40° + 0.7/50° + 0.8/60° + 0.9/70° + 1.0/80° + 1.0/90° .
Нечеткий вывод “Если высокий, то открыть” реализуется в данной системе на основе формул (6.3) и (6.4), как показано на рис. 6.6. Управление происходит в три этапа:
-фаззификация - превращение уровня выдаваемого датчиком (например 1.75 м) в лингвистическую переменную (в данном случае A’ - довольно высокий), представленную на рис. 6.6.(а) в виде множества m_A(x) с учетом разброса измеряемого параметра x;
-реализация нечеткого вывода по формуле полученной из (6.3) и (6.4) b_j’=И _i(a_i’o a_i)З b_j, (6.5) Как показано на рис. 6.6 (б) и (в);
-дефаззификация, то есть превращение полученного выходного множества m_B’(y) в выходную величину y. В данном случае на рис. 6.6, (в) показана дефаззификация по методу центра тяжести (фигуры заштрихованной на рис. 6.6, (в), который дает y’=70° .

Рис. 6.6 Реализация управления в простейшей Fuzzy-системе.

6.2. Реализация нечеткого управления.

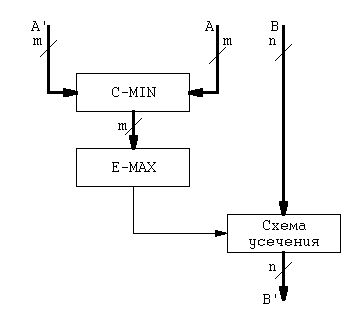
Нечеткое управление может быть реализовано специальными нечеткими контроллерами, в основе которых лежит так называемая машина нечетких выводов, структура которой показана на рис. 6.7.[8].
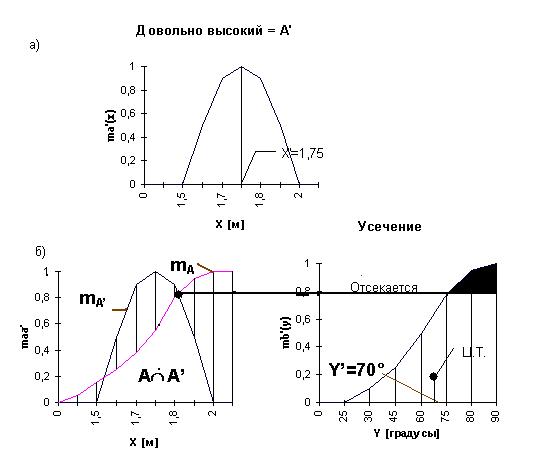
Эта машина реализует нечеткий вывод типа “Если А, то В” по формуле (6.5), как показано на рис. 6.6. Блок, реализующий функцию C-MIN, осуществляет пересечение множеств А и А’. Блок, реализующий функцию E-MAX, выделяет из множества А? А’ элемент с максимальным значением, который осуществляет усечение множества В, превращая его во множество В’
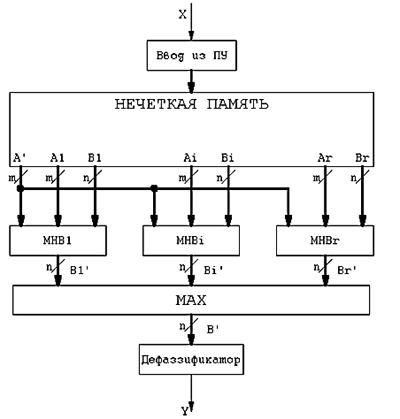
. Базовая архитектура нечеткого контроллера, выполняющего много нечетких выводов (r), содержит r машин нечетких выводов (МНВ), как показано на рис. 6.8. Кроме МНВi базовый нечеткий контроллер содержит нечеткую память в которой хранится база знаний и схема объединения результатов выводов - MAX с дефаззификатором.

Рис. 6.7. Функциональная схема машины нечетких выводов.

Рис. 6.8. Базовая архитектура нечеткого контроллера.

Нечеткое управление может быть реализовано с помощью обычных или специализированных логико-арифметических контроллеров, в которых нечеткие выводы выполняются путем вычисления характеристических значений выходной лингвистической переменной через характеристические значения входных лингвистических переменных по логическим формулам использующим логические операции “И” и “ИЛИ”.

Переход от лингвистических переменных, принимающих различные лингвистические значения - ТЕРМЫ, производится через соответствующие характеристические функции - функции принадлежности, показанные на рис. 6.9. Считается, что для реализации простейших алгоритмов нечеткого управления достаточно, чтобы каждая лингвистическая переменная содержала от 3 до 7 термов.
Z-функция p -функция l -функция S-функция

Рис. 6.9. Типовые функции принадлежности.

Разработка алгоритма нечеткого управления традиционно содержит три этапа:

Этап 1. Фаззификация - переход от физических переменных к лингвистическим переменным и их характеристическим функциям. Фаззификация может быть осуществлена путем выполнения следующих шагов:
Шаг 1. Для каждого терма взятой лингвистической переменной находится числовое значение физической величины (или диапазон значений), наилучшим образом характеризующей данный терм и этим значениям присваивается характеристическое значение равное “1”.
Шаг 2. Для каждого терма выбирается диапазон значений физической переменной при которых характеристическая функция принимает значение “0”.
Шаг 3. После определения экстремальных значений определяются промежуточные значения характеристических функций путем выбора типовых функций, показанных на рис. 6.9.
Этап 2. Построение нечетких правил.
Большинство нечетких систем используют продукционные правила для описания зависимостей между лингвистическими переменными. Типичное продукционное правило состоит из антецедента (часть ЕСЛИ...) и консеквента (часть ТО...). Антецедент может содержать более одной посылки. В этом случае они объединяются посредством логических связок “И” или “ИЛИ” т.е. операндов MIN/MAX. Сам процесс вычисления нечеткого правила носит название нечеткого логического вывода и подразделяется на два этапа: обобщение и заключение.
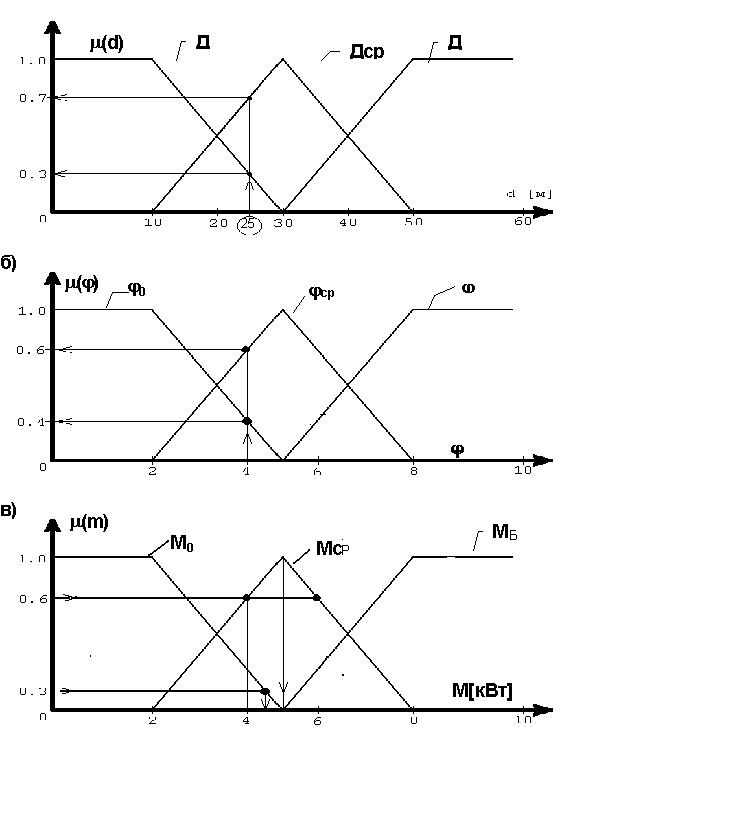
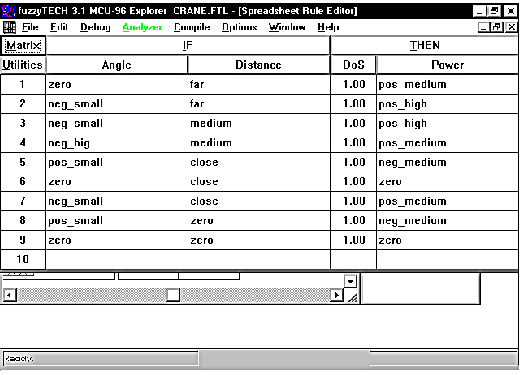
Например, для системы управления башенным краном, функциональная схема которой показана на рис. 6.10, входными переменными являются расстояние (дистанция) от каретки до стены d[м], и угол отклонения груза от вертикали j ° , а выходной переменной - мощность, подаваемая на двигатель каретки m. Допустим, что каждая из этих переменных имеет три терма - нулевое, среднее и большое, которым соответствуют свои характеристические величины:

Рис. 6.10 Функциональная схема управления башенным краном. D₀ - нулевое (малое) расстояние;
D_ср - среднее расстояние;
D_б - большое расстояние;
j ₀ - нулевой (малый) угол;
j _ср - средний угол ;
j _б - большой угол;
М_{0 -}нулевая (малая) мощность;
М_ср - средняя мощность;
М_б - большая мощность; Все эти величины принимают значения на интервале {0-1}.
Тогда, например, одно из продукционных правил может быть следующим:
ЕСЛИ Дистанция=средняя И Угол=малый, ТО Мощность=средняя.
С учетом введенных выше обозначений это правило можно представить в виде логической формулы М_ср = D_ср_{j
0 = min[Dср},j ₀]. После вычисления всех правил получается нечеткое значение выходной переменной в виде степеней принадлежности ее термов. В данном примере - М₀, М_ср, М_б. Чтобы исполнительное устройство могло срабатывать, необходимо перейти от степеней принадлежности к значению выходной физической величины (в данном случае мощности m). Этот процесс носит название дефаззификации.
Этап 3. Дефаззификация.
Наиболее распространены три способа дефаззификации:
-метод центра максимума (CoM), при котором выходная величина является средним значением величины, полученной через вычисленные степени принадлежности - m₀, m_ср, m_б; т.е. m=(1/3)(m₀+m_ср+m_б);
-метод набольшего значения (MoM), при котором выбирается наибольшее значение из полученных, т.е. m=MAX(m₀,m_ср,m_б);
-метод центроида (CoA), при котором значение выходной величины является координатой центра тяжести фигуры, получаемой усечением характеристических функций выходной величины полученными значениями их степеней принадлежности.
Рассмотрим более подробно разработку алгоритмов функционирования системы управления башенным краном.

Этап 1. Фаззификация.
На этом этапе разрабатываются функции принадлежности для всех трех переменных, показанные на рис. 6.11.
Этап 2. Построение продукционных правил.
Перечислим все возможные комбинации входных переменных

D₀j₀, D₀j_ср, D₀j_б, D_срj_б; - М₀ D_срj₀_, D_срj_ср, D_бj_б; - М_ср D_бj₀_,D_бj_ср; - М_б

Разобьем их на три группы, соответствующие трем термам выходной переменной, например, так, как показано выше.
На основании этого разбиения можем написать формулы, соответствующие продукционым правилам вычисления выходных переменных

М₀=D₀ ИD_срj_б=max[D₀; min(D_срj_б)] (6.6) М_ср=D_срj_срИD_бj_б=max[min(D_срj_ср); min(D_бj_б)] М_б=D_б(j₀Иj_б)=min[D_б_;max(j₀j_ср)]

Произведем вычисления для конкретных значений d=25м и j =4° ,
см. табл. 6.1.
Результаты вычисления по формулам (6.6)

Таблица 6.1.

j ₀	j _ср	j _б	D₀	D_ср	D_б	М₀	М_ср	М_б
0.4	0.6	0	0.3	0.7	0	0.3	0.6	0

М₀=max[0.3 ; min(0.7;0)]=0.3 М_ср=max[min(0.7;0.6); min(0;0)]=0.6 М_б=min[0; max(0.4;0.6)]=0

Этап 3. Дефаззификация.
Принцип дефаззификации показан на рис. 6.11.в),:
-по методу CoM получим m=4.5 квт;
-по методам MoM и CoA m=5 квт.
Таким образом, при принятых значениях входных переменных d и j надо подавать на двигатель среднюю мощность, так как величина степени принадлежности этого терма преобладает над другими.

а)

Рис. 6.11. Функции принадлежности входных (а,б) и выходной (в) величин системы управления башенным краном. 6.3.Проектирование систем управления динамическими объектами с использованием алгоритмов нечеткой логики на стандартных микроконтроллерах.

После бурного старта прикладных нечетких систем в Японии, многие разработчики в США и Европе обратили внимание на новую технологию. Но к этому моменту время было упущено и мировым лидером в области нечетких систем стала Япония. К концу 80-х годов в этой стране был налажен выпуск специализированных нечетких контроллеров выполненных по технологии СБИС. Догонять японцев значило потерять массу времени. Поэтому фирмой Intel было принято альтернативное решение. Имея большое количество разнообразных контроллеров от MCS-51 до MCS-96, которые на протяжении многих лет успешно используются во многих приложениях, Intel решила предоставить разработчикам средство разработки приложений на базе этих контроллеров, но с использованием технологии нечеткости. Создание подобной системы позволило избежать значительных затрат на создание собственных нечетких контроллеров, а разработанная система, получившая название fuzzyTECH, завоевала огромную популярность не только в США и Европе, но и в Японии.
Сейчас существует много версий fuzzyTECH. Все они различаются как по своим возможностям, так и по своей цене. Самый простой из семейства fuzzyTECH - это пакет fuzzyTECH Explorer Edition. Explorer - это великолепное средство обучения. Он предоставляет пользователю большие возможности по практическому освоению нечеткой технологии. Существует и более мощный профессиональный пакет fuzzyTECH MCU-96, ориентированный на микроконтроллеры Intel семейства MCS-96. Еще один вариант - это fuzzyTECH On-line Edition. Этот пакет позволяет отлаживать готовую систему, отлавливая ошибки прямо “на лету”. В приложениях, работающих в реальном масштабе времени, это незаменимое средство отладки. Профессиональные редакции fuzzyTECH поддерживают многие из последних достижений нечеткой технологии: арбитражные функции принадлежности, современные методы дефаззификации и многое другое.
FuzzyTECH - это полностью графическое средство поддержки разработки приложений на основе нечеткой логики. Это средство моделирования и оптимизации всего проекта. Обладает совместимостью с обычными средствами разработки. Графическое представление на экране всех стадий разработки позволяет найти множество путей оптимизации проекта. Наконец, это генератор кода, который поддерживает большинство современного оборудования, при этом разрабатываемый код может быть сгенерирован как код языка C. Ассемблерный код весьма функционален, точно соответствует возможностям применяемого аппаратного обеспечения и типу микроконтроллера.
Обычно выделяется пять стадий разработки проекта с помощью fuzzyTECH:

Формализация поставленной задачи (определение лингвистических переменных, сопоставление термов с конкретными физическими значениями);
Разработка базы правил, определяющих стратегию управления (задание метода дефаззификации выходных данных);
Оптимизация разработанной системы в режиме off-line (интерактивный анализ поведения системы с использованием заранее подготовленных данных или при помощи программной модели объекта управления);
Оптимизация в режиме on-line (подключение созданной системы управления к реальному объекту и оптимизация различных компонентов системы в реальных условиях; так как в модели объекта управления невозможно учесть все тонкости процесса, то данный режим отладки весьма важен при создании систем управления);
Реализация (выбирается вариант генерируемого кода; полученный код для микропроцессора может быть связан с основной программой либо записан в ПЗУ системы управления).

При использовании пакета fuzzyTECH все шаги разработки осуществляются посредством нажатий кнопок мыши. Внутренняя работа fuzzyTECH проводится с использованием языка FTL (Fuzzy Technology Language). FTL - это аппаратно независимый объектно-ориентированный язык для разработки нечетких систем. Он имеет открытую архитектуру и может быть расширен в зависимости от потребностей пользователя.
Работа над созданием fuzzyTECH началась в середине 80-х годов исследовательской группой под руководством профессора Ганса Циммерманна (Hans Zimmermann), который более 20 лет является наиболее известным специалистом в области теории нечетких множеств. Первая версия пакета появилась в 1990 году. В настоящий момент существует версия для MS-Windows 3.1. Для ее запуска требуется 386 (или выше) PC с графическим адаптером VGA, DOS 5.0 (или выше) и MS-Windows 3.1 (или выше), запущенная в расширенном режиме. Так как fuzzyTECH интенсивно использует графику, то рекомендуется цветной графический монитор с разрешением 800x600 или 1024x768. Для цветных графиков рекомендуется 256-цветный графический режим. Все функции fuzzyTECH доступны с клавиатуры, следовательно мышь не обязательна (но очень желательна). FuzzyTECH производится немецкой фирмой INFORM, которая имеет отделения в Германии, США и Японии.
Система Разработки fuzzyTECH содержит:

Редакторы (Editors).
Отладчик (Debugger).
Анализатор (Analyzer).
Генератор Кодов (Code Generation) для реализации нечетких систем.
Опции (Options) используются, чтобы сконфигурировать инструментальные средства.

FuzzyTECH использует стандартные MS-Windows функциональные назначения.
FuzzyTECH может использоваться с мышью или клавиатурой. Обычно, объект выбирается единственным нажатием кнопки мыши. Двойное нажатие на объекте обычно активизирует окно редактирования свойств объекта. Используя клавиатуру, [Ctrl][F6] клавиши позволяют переключать фокус между окнами основного окна. Внутри окна, [ТАБ] выбирает разные группы. Используйте клавиши управления курсором, чтобы перемещаться внутри группы и клавишу [Enter], чтобы активизировать ту или иную опцию. Некоторые объекты, как например, определенные точки в редакторе лингвистических переменных или объекты редактора проекта, могут быть перемещены внутри окна. Для того, чтобы разместить эти объекты с помощью клавиатуры, сначала выберите объект, который нужно переместить используя [ТАБ], активизируйте его [Enter] и переместите клавишами управления курсором и установите его, снова нажав [Enter].
Каждое окно в fuzzyTECH имеет собственное всплывающее меню для опций доступных только для этого окна. Для того, чтобы сделать доступным меню или нажмите над соответствующим окном правой кнопкой мыши или используйте клавишу [Shift] вместе с нажатием левой кнопки мыши. [Shift][F10] или [F9] также могут использоваться для доступа к меню.
При запуске, fuzzyTECH открывает два окна - Окно Редактора Проекта и Окно Лингвистических Переменных (LV) (рис. 6.12). Только одно окно редактора проекта и одно LV-окно могут быть открыты одновременно. Ни одно из этих окон не может быть закрыто в течение сеанса работы с fuzzyTECH, но столько окон лингвистических переменных (LV) можно открыть, сколько определено переменных. Редактор Проекта содержит структуру системы нечеткой логики, то есть интерфейсы и блоки правил в то время как LV-окно содержит список всех лингвистических переменных системы.
Большинство возможностей редактирования доступны из различных окон редактирования с помощью всплывающих меню:
LV Окно:

Редактор Лингвистических Переменных
Окно Определения Базовой Переменной (Base Variable Dialog Box)
Окно Определения Терма (Term Dialog)

Редактор проекта:

Окно Определения Блока Правил (Rule Block Dialog)
Табличный Редактор Правил (Spreadsheet Rule Editor)
Матричный Редактор Правил (Matrix Rule Editor)
Окно Определения Опций Интерфейса (Interface Options Dialog)
Окно Определения Замечаний (Remark Dialog)

Лингвистические Переменные указываются в алфавитном порядке в

Рис. 6.12. Вид окна fuzzyTECH при запуске системы.

LV-окне. LV-окно всегда открыто и может быть свернуто до пиктограммы, но не закрыто. LV-окно содержит все лингвистические переменные текущего проекта по именам в алфавитном порядке. Если нужно всегда указывать переменные в другом порядке, продолжите все имена переменных буквами, например 'AA_FirstVar', 'AB_SecVar'.
В нечеткой логике, различные величины для данной лингвистической переменной представляют собой понятия, а не числа. В нечеткой логике, даже приближенные описания такие как “чрезвычайно близко” и “очень далеко” возможны, поскольку каждый лингвистический терм представлен специфическим нечетким множеством, названным Функцией Членства.
Конечно, техническая величина измерима как точная. Степень с которой точная величина принадлежит ко множеству представлена числом, лежащим между 0 и 1. Эта величина названа Степень Членства (или степень принадлежности) (Membership Function - MBF). 0 означает, что переменная определенно не принадлежит ко множеству; 1 отражает абсолютное членство. Величины между 0 и 1 представляют частичное членство, таким образом учитываясь в выражениях, которые частично истинны и частично ложны (задание, которое невозможно выполнить используя стандартную логику). В нечеткой логике, Степень Членства обычно нормирована в интервале [0; 1]. Технические цифры представлены на горизонтальной оси функции, а степени членства на вертикальной. Технические цифры названы базовой переменной. Хотя научные публикации предложили много разных типов функций членства для нечеткой логики, в большинстве практических приложений используются Стандартные Функции Членства. Стандартные Функции Членства могут быть в общем представлены L-формой определения. Научные исследования предлагают несколько иной подход к этой задаче. Он базируется на психо-лингвистическом исследовании человеческой классификации длительных переменных, получающим S-форму функции членства. Пока большинство приложений использует стандартные MBF через S-тип MBF, хотя некоторые методы вывода функций членства и некоторая техника адаптации требует более общих функций. Для удобства проектирования этих типов функций членства и для наиболее эффективного динамического кодового представления, функции произвольного членства наилучшим образом приближенно представимы как линейные многоугольники. Стандартные функции членства - Z, Лямбда, Pi и S-типы (рис. 6.9). Все эти типы стандартных функций математически могут быть представлены как часть функций - линейных многоугольников с вплоть до 4 определяющих точек. FuzzyTECH позволяет определять ассиметричный характер параметра "форма". Имейте в виду, что S-типа функции членства требуют больше динамического кода и больше вычислительного времени, если они не сохранены как таблицы.
Фаззификация означает оценку всех степеней членства в точке специфической операции. Результат фаззификации используется в качестве входа для Нечетких Правил. Если переменная используется в качестве выходной в нечеткой системе, лингвистические термы могут быть вновь переведены в точные физические величины. Эти вычисления названы дефаззификацией.
В большинстве приложений, количестве используемых термов - между 3 и 7. Менее чем 3 используемых терма - редкое явление вследствие того, что, когда люди оценивают реальные числа, те которые имитируют лингвистические переменные, они обычно имеют по крайней мере три величины в уме - два предела и середина. Количество используемых термов редко превышает 7 поскольку оценка чисел включает краткосрочную память, которая лучше всего работает с не более чем 7 символическими величинами. Переменные с “центром” или “нулем” наилучше работают с нечетным количеством термов (рис. 6.13).
Есть в основном два разных метода для определения подходящего количества термов для данной проблемы. Для разработчиков с некоторым опытом в создании нечетких систем, один метод - сформулировать примерные правила даже перед проектированием функций членства. Это

Рис. 6.13. Вид окна fuzzyTECH-редактирование термов.

учитывается при быстрой оценке - сколько термов должны использо-ваться? Для пользователей без предшествующего опыта в разработке нечетких систем или если примерные правила легко не формулируются, наилучший метод - во-первых, создать три терма (два предела и середина). Если большее термов нужно создать в течении разработки, то они могут легко быть добавлены при использовании fuzzyTECH.
Большинство нечетко-основанных систем используют продукционные правила, чтобы представить отношения между лингвистическими переменными и получить данные от входов. Продукционные правила состоят из условия (ЕСЛИ-часть) и вывода (ЗАТЕМ-часть). ЕСЛИ-часть может состоять из более чем одного предусловия, компонуемых вместе лингвистическими конъюнкциями (И и ИЛИ) (рис. 6.14).
Используя стандартные MAX-MIN/MAX-PROD методы, оптимизация базового правила часто состоит из произвольного дополнения/удаления правила. Этот метод может дать результат по методу проб и ошибок так как индивидуальное значение правила может быть выражено только как 0 или 1. По этой причине, большинство редакций fuzzyTECH поддерживают усовершенствованную стратегию вывода - Нечеткие Ассоциативные Карты (FAM). С FAM, каждое правило наделено Степенью Поддержки (DoS), представляющей индивидуальное значение правила. Таким образом правила сами могут быть "нечетки" - знача, с достоверностью между 0 и 1. Если работа с нечеткими технологиями только начинается, то используйте правила со степенью поддержки только 0 и 1.

Рис. 6.14. Вид окна fuzzyTECH-редактирование правил.

Достоверность вывода вычисляется компоновкой достоверности условия в целом со степенью поддержки оператором композиции. Когда продукционный оператор используется в качестве оператора композиции, степень поддержки отражает “значение” правила.
Результат, полученный из оценки нечетких правил - нечеткий. Функции Членства используются, чтобы вновь перевести нечеткий вывод в точную величину. Этот перевод известен как дефаззификация и может быть выполнен с использованием различных методов.
Дефаззификация, используемая редакциями fuzzyTECH:

CoM - Центр Максимума - метод используется для большинства нечетких логических приложений.
CoA - Центр Области - метод подобен CoM.
MoM - Значение Максимума - метод используется для приложений распознавание образов.
MoM BSUM и CoA BSUM - варианты MoM и CoA, которые оптимизировались для реализации эффективных СБИС.

Опция Нечеткий Выход подавит процедуру дефаззификации при использовании генерации кода.
Методы дефаззификации CoM и CoA дают в результате “наилучшее компромиссное решение”, MoM дает в результате "большинство правдоподобных решений". В управляющих приложениях, CoM - наиболее часто используется, поскольку выходная величина представляет наилучший компромисс между всеми результатами логического вывода. MoM часто используется в распознавании образов и приложениях классификации и правдоподобное решение будет здесь наиболее подходящим. Научная литература предложила многие другие стратегии дефаззификации, которые до сих пор редко использовались в промышленных приложениях. Поскольку fuzzyTECH также учитывает пропуск дефаззификации, может также использоваться метод дефаззификации определяемый пользователем.
В целом fuzzyTECH является удачной разработкой, сильно облегчающей проектирование микропроцессорных систем управления, основанных на нечеткой технологии.

Литература:

Микропроцессорные системы автоматического управления / Бесекерский В.А. и др. - Л.:Машиностроение, Лен. отд., 1988 - 365с.
Боборыкин А.В. и др., Однокристальные микроЭВМ, М.:МИКАП, 1994
Гребнев В.В., Однокристальные микроЭВМ (микроконтроллеры) семейства MCS-96, 1995
Микропроцессоры в системах автоматического управления. INTEL 8XC196MC: Учеб. пособие / Бутырин Н.Г. и др.: СПбГТУ, СПб., 1995, 115с.
Изерман Р., Цифровые системы управления: пер. с англ. - М.: Мир, 1984 - 541с., ил.
Микропроцессорное управление электроприводами станков с ЧПУ. / Тихомиров Э.Л. и др. - М.: Машиностроение, 1990
Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений., М.: Мир, 1976, 165с.
Прикладные нечеткие системы / Тэрано Т., Асаи К., Сугено М., 1993