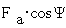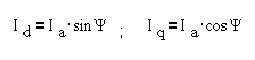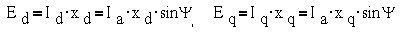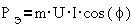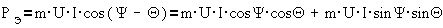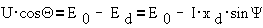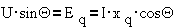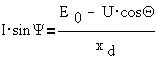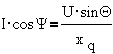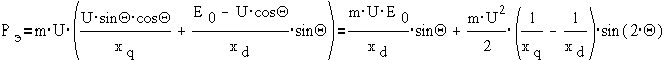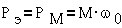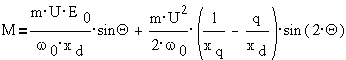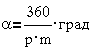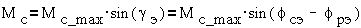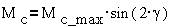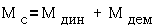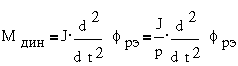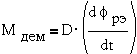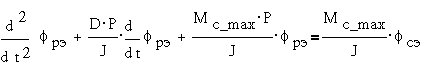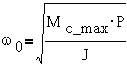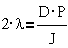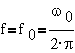ГЛАВА 4. СИНХРОННЫЕ МАШИНЫ

4.1. Электромеханическое преобразование энергии в синхронных машинах

Синхронной машиной называется двухобмоточная электрическая машина переменного тока, одна из обмоток которой возбуждается с частотой ω1, а вторая - постоянным током.

Наибольшее распространение получили трехфазные синхронные генераторы большой мощности.

В синхронных микромашинах для образования поля возбуждения часто используются постоянные магниты.

В зависимости от формы магнитной системы ротора синхронные машины бывают явнополюсными и неявнополюсными.

Рассмотрим электромеханическое преобразование энергии в синхронной машине на примере однопериодной модели явнополюсного синхронного генератора, схема которого показана на .

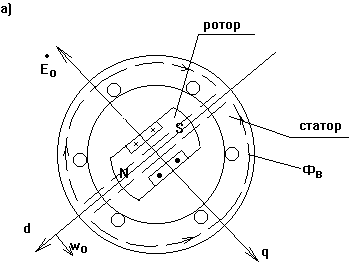
Рис. 4-1а,б. Схема явнополюсного синхронного генератора.

Такая машина имеет трехфазную обмотку на статоре и двухполюсный ротор, на котором находится обмотка возбуждения. Протекающий по этой обмотке ток возбуждения создает МДС F0, направленную по предельной оси ротора d и соответственно поток возбуждения Ф0 (см. ). При вращении ротора в обмотках статора возникает переменная ЭДС синусоидальной формы и частоты ω1=ω. Эту ЭДС можно представить в виде вектора E`0, вращающегося с частотой ω и направленного перпендикулярно вектору потока возбуждения Ф`0.

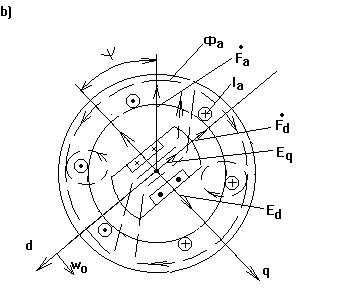
Однопериодная модель машины удобна тем, что в ней временные и пространственные углы между векторами совпадают, что дает возможность наложить временную векторную диаграмму токов и напряжений на пространственную картину полей в машине, как это сделано на .

При подключении обмоток якоря (статора) к нагрузке в них под действием ЭДС E0 возникает переменный ток якоря Ia, который создает переменный магнитный поток реакции якоря Фa, как показано на . Поле реакции якоря накладывается на поле возбуждения, искажая его и изменяя, таким образом, вектор E`0 как по величине, так и по направлению. В нагруженной машине возникает сложная картина вращающегося магнитного поля, вследствие чего анализ процессов весьма затруднителен.

Для ненасыщенной машины справедливы линейные зависимости между МДС, потоком и ЭДС, поэтому применим принцип суперпозиции, т.е. можно рассматривать отдельно поле возбуждения и возникающие при этом ЭДС и поле реакции якоря и ЭДС, возникающие от его вращения, а затем производить векторное сложение ЭДС.

Будем считать, что генератор нагружен на активно-индуктивную нагрузку (как это обычно бывает). Тогда ток якоря Ia отстает по фазе от основной ЭДС E0 на угол Ψ, как показано на . Этот ток создает в магнитной системе машины МДС Fa, вектор которой показан на . Для того, чтобы оценить влияние МДС реакции якоря Fa на основную ЭДС E0, производят разложение вектора на две составляющих, направленных вдоль продольной и поперечной осей ротора:

,    

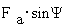
Этим МДС соответствуют токи Id и Iq, для которых справедливы аналогичные формулы:

.

Эти токи создают ЭДС продольной и поперечной реакции якоря, которые отстают от своих МДС на угол 90 градусов, и, таким образом, ЭДС продольной реакции якоря направлена вдоль поперечной оси, а ЭДС поперечной реакции, наоборот, вдоль продольной оси ротора, как показано на . Эти составляющие ЭДС реакции якоря можно выразить через ток якоря Ia:

где xd и xq называются синхронными индуктивными сопротивлениями машины по продольной и поперечной осям.

Если пренебречь индуктивностью рассеяния и активным сопротивлением обмоток якоря, получим упрощенную эквивалентную схему цепи якоря (). Временная векторная диаграмма якорной цепи для этого случая приведена на .

Рис. 4-2а. Упрощенная эквивалентная схема якорной цепи синхронной машины.

Рис. 4-2б. Временная диаграмма якорной цепи синхронной машины.

Электромагнитная мощность синхронной машины может быть записана как

где U и I- фазное напряжение и фазный ток машины, m- число фаз.

Согласно упрощенной векторной диаграмме машины ()

.

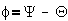
Подставляя в выражение () получим

Однако из диаграммы следует

Отсюда

Подставляя эти выражения в (), получим

Электромагнитная энергия состоит из двух составляющих: первая является энергией вращающегося магнитного поля, создаваемого обмоткой возбуждения с учетом его искажения реакцией якоря, а вторая - энергией несимметрии вращающихся полей продольной и поперечной реакций якоря.

В идеальной модели электромагнитная энергия превращается в механическую (или наоборот), т.е.

Отсюда может быть получено выражение для электромагнитного момента, также как суммы двух составляющих

Первая составляющая момента - это магнитоэлектрический момент, вызванный воздействием поля возбуждения с вращающимся магнитным полем, вторая составляющая - так называемый реактивный момент, который создается а счет изменения индуктивности системы при повороте ротора, т.е. неравенства магнитных сопротивлений по осям d и q.

Существуют машины, в которых используется только первая составляющая момента - магнитоэлектрические машины, либо только вторая составляющая - реактивные машины.

4.2. Специальные синхронные двигатели

Синхронные двигатели небольшой мощности применяются в системах автоматики. Поскольку в синхронных двигателях частота вращения жестко связана с частотой питания, такие двигатели применяются либо в системах, требующих строго постоянной частоты вращения, либо при частотном управлении скоростью.

К группе синхронных двигателей можно отнести также двигатели, частота питания которых зависит от частоты вращения - это так называемые вентильные двигатели. Но поскольку они имеют коммутатор и их характеристики похожи на характеристики двигателей постоянного тока, они будут рассмотрены в главе 5.

В цифровых системах автоматики находят широкое применение шаговые двигатели, в обмотки статора которых поступают импульсы тока и при поступлении каждого импульсов происходит поворот ротора на определенный угол - двигатель совершает шаг. В зависимости от особенностей возбуждения шаговые двигатели, как и другие типы синхронных двигателей, делятся на двигатели с активным ротором, представляющим собой явнополюсный ротор из постоянного магнита, и с реактивным ротором, представляющим собой явнополюсный или зубчатый ротор из магнитомягкого материала.

Рассмотрим более подробно принцип действия и характеристики шаговых двигателей.

Статор шаговых двигателей в отличие от синхронных микродвигателей непрерывного вращения имеет явновыраженные полюсы, на которых располагаются обмотки управления. Число пар полюсов каждой из обмоток управления p равно числу пар полюсов ротора.

Наибольшее развитие получили ШД активного типа - с ротором, содержащим многополюсный постоянный магнит.

Принцип действия такого ШД рассмотрим на примере двухфазной двухполюсной конструкции ().

Рис. 4-3а. Схема шагового двигателя.

Этот двигатель имеет две взаимно перпендикулярные обмотки А и В, в которые могут подаваться импульсы тока разной полярности, как показано на .

Рис. 4-4. Временная диаграмма работы ШД.

Наличие тока в обмотке создает магнитный поток статора Ф0, который поворачивается при переключении обмоток на угол α. Вслед за потоком поворачивается и активный ротор, т.е. при каждом переключении двигатель делает шаг. Полный оборот потока совершается за m-тактный (в данном случае четырехтактный) цикл.

В общем случае для двигателя с активным ротором шаг двигателя

где p- число пар полюсов, m- число тактов управления.

Поворот ротора совершается под действием так называемого синхронизирующего момента, который возникает при отклонении ротора от направления потока на угол γ, как показано на .

Часто вводят понятие электрических углов, при которых многополюсных двигатель сводится к двухполюсной (однопериодной) модели. Для двигателей с активным ротором

; .

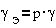
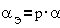
Электрический угол γэ эквивалентен внутреннему углу синхронной машины Θ в формуле . Тогда согласно в ШД с активным ротором, где преобладает магнитоэлектрический момент

,

где Mc_max- максимальный синхронизирующий момент, fсэ и fрэ- электрические углы поворота МДС статора и оси ротора.

При переключении фазы происходит сдвиг статической характеристики на угол αэ, как показано на .

Рис. 4-3в. Статическая характеристика шагового двигателя.

Возникает пустой момент Mп, под действием которого происходит поворот ротора в согласованное с магнитным потоком положение. Если двигатель нагружен внешним магнитом MB, то ротор переходит из точки 1 в точку 3 по траектории 1-2-3. Для того, чтобы при переключении обмотки происходил поворот ротора, необходимо выполнение условия MП≥MB. Отсюда существует допустимый внешний момент Mдоп и соответствующий ему допустимый угол отклонения оси ротора от направления потока γэ_доп, при которых МП=МВ=МДОП. Чем больше ШД имеет фазных обмоток и соответственно тактов переключения, тем меньше у него шаг γэ и соответственно больше МДОП. Поэтому обычно ШД являются многофазными (от 3-х до 6-ти фаз). По этой причине, как видно из , двухфазный ШД с пассивным ротором вообще не работоспособен.

Рис. 4-3г. Схема шагового двигателя.

Рис. 4-3д. Статическая характеристика шагового двигателя.

Рис. 4-3е. Статическая характеристика шагового двигателя.

Так, у него согласно вращающий момент определяется реактивной составляющей

и статическая характеристика имеет вид, показанный на .

Отсюда соотношения для электрических и геометрических углов поворота ротора будут

; ,

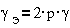
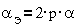
т.е. для двухфазного ШД p=1,α=90·град, а αэ=180·град, сдвиг характеристики при переключении фазы происходит на 180 градусов, как показано на и ротор не поворачивается, так как пусковой момент равен нулю.

Физически это можно объяснить тем обстоятельством, что при пассивном роторе направление синхронизирующего момента не зависит от направления потока. Момент равен нулю и в том случае, когда поток направлен вдоль полюсов и когда поперек полюсов, и достигает максимума, когда ось ротора располагается между полюсами статора, в отличие от активного ротора, в котором момент максимален, если поток направлен поперек ротора. Поэтому реактивные ШД должны иметь как минимум три обмотки и трехтактную систему коммутации.

Существуют различные режимы работы ШД:

Статический режим соответствует прохождению постоянного тока по обмоткам управления, создавая неподвижное магнитное поле. Основной характеристикой этого режима является статическая характеристика MC=f(γэ), рассмотренная ранее ().

Режим отработки единичных шагов соответствует частоте управляющих импульсов, при которой переходный процесс, чаще всего колебательный, на каждом шаге заканчивается к началу следующего шага, т.е. угловая скорость ротора f`р в начале каждого шага равна нулю (см. ).

Рис. 4-5. Отработка единичных шагов.

Основными показателями этого режима являются: перерегулирование Δfп, максимальное значение мгновенной угловой скорости f`p_max, время затухания свободных колебаний ротора tзат.

Если время электромагнитных переходных процессов значительно меньше, чем механических, движение ротора ненагруженного ШД можно описать следующим уравнением

,

где Mдин- динамический момент, Мдем- демпфирующий электромагнитный момент.

Динамический момент определяется моментом инерции ротора и ускорением:

Внутреннее электромагнитное демпфирование колебаний ротора происходит за счет поведения ЭДС вращения в обмотках управления. Значение демпфирующего момента пропорционально угловой скорости ротора:

,

где D- коэффициент демпфирования.

Если рассматривать работу ШД при малых углах рассогласования осей ротора и МДС статора (sin(γ)≈ γ), то, подставив , и в , получим дифференциальное уравнения движения ротора:

В этом выражении коэффициент при fрэ есть квадрат угловой частоты собственных колебаний ротора

,

а коэффициент при f`рэ характеризует относительный коэффициент затухания колебаний λ:

.

Установившийся режим работы ШД соответствует постоянной частоте управляющих импульсов f, причем 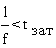. В установившемся режиме вращение ротора с некоторой средней угловой скоростью ω сопровождается вынужденными колебаниями.

Амплитуда колебаний достигает наибольшего значения при частоте управляющих импульсов, совпадающей с резонансной - собственной частотой ротора:

Важной характеристикой установившегося режима является предельная механическая характеристика, представляющая собой зависимость допустимого момента сопротивления от частоты управляющих импульсов. Предельную механическую характеристику рассматривают обычно при f>f0 ().

Рис. 4-6а. Предельные механические характеристики ШД.

Снижение MДОП при увеличении f объясняется в основном наличием электромагнитной постоянной времени Tу обмоток управления

,

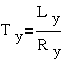
где Rу и Lу- активное сопротивление и индуктивность обмоток управления. Последнее объясняется тем, что чем больше Tу, тем меньше за время импульса нарастает ток, что снижает синхронизирующий момент. Снижение напряжения питания также уменьшает MДОП.

Переходные процессы - пуск, торможение, реверс, переход с одной частоты на другую - сопровождаются переходными процессами в ШД.

Важным показателем переходного режима является приземистость ШД - наибольшая частота управляющих импульсов, отрабатываемая ШД для потери шага - частота приемистости fпр.

Приемистость растет с увеличением синхронизирующего момента, а также с уменьшением шага, момента инерции и статического момента сопротивления (см. , где МВ- внешний момент сопротивления типа трения).

Рис. 4-6б. Предельные динамические характеристики ШД.

4.3. Упражнения и контрольные вопросы к главе 4.

  1. Аналогично рис. 4-3, а и б построить картину магнитного поля и установившегося положения ротора ШД при одновременной запитке двух обмоток статора.
    2.
  2. Аналогично рис. 4-3, в построить статические характеристики ШД для режима последовательного включения одной обмотки и пары обмоток. Определить для этого режима Мдоп и gэдоп .
  3. Для четырехфазного ШД типа ДШ78-0,16-1 определить собственную частоту колебаний fо. (Параметры двигателя: Мсмакс=0,56 Нм; J=0.00001 кг м**2; a=1 град.).