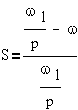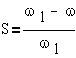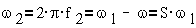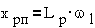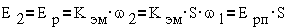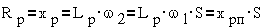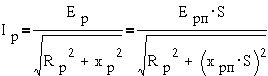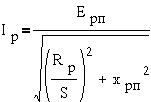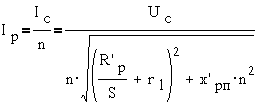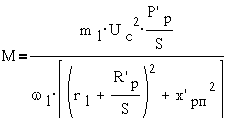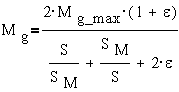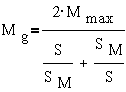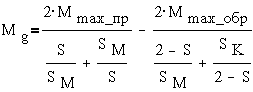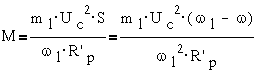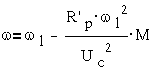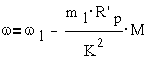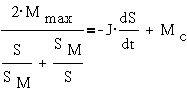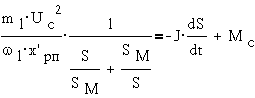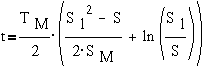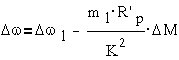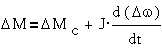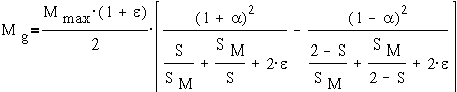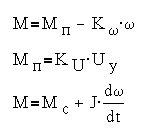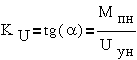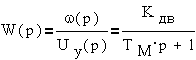ГЛАВА 3. АСИНХРОННЫЕ МАШИНЫ
- 3.1. Общие с сведения
и электромеханическое преобразование энергии в асинхронных машинах
- 3.2. Асинхронные
трехфазные двигатели
- 3.3. Асинхронные
двухфазные управляемые двигатели
- 3.4. Упражнения и контрольные
вопросы к главе 3.
3.1. Общие с сведения и
электромеханическое преобразование энергии в асинхронных машинах
Как указывалось
выше, асинхронной машиной называется машина переменного тока, у которой только
первичная обмотка получает питание от электрической сети с постоянной частотой,
а вторая обмотка замыкается накоротко или на электрическое сопротивление. Токи
во вторичной обмотке появляются в результате электромагнитной индукции. Их
частота ω зависит от угловой скорости вращения ротора ω.
Асинхронные машины используются
в основном как двигатели, в качестве генераторов они применяются крайне редко.
Наибольшее распространение получили трехфазные асинхронные двигатели с
короткозамкнутым ротором, имеющие трехфазную обмотку на статоре и питающиеся от
трехфазной сети. Трехфазный асинхронный двигатель является наиболее
распространенным двигателем постоянного тока.
В системах
автоматического управления используются двухфазные асинхронные двигатели с
короткозамкнутым, чаще всего с немагнитным полым ротором.
В асинхронных
машинах обмотки статора, питающиеся переменным током частоты 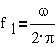
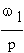
индуктируются
вторичные ЭДС e2 и токи i2 частоты ω2,
которые взаимодействуют с вращающимся магнитным полем, создается
электромагнитный момент M, что приводит к вращению
ротора с частотой ω1.
Скорость вращения
ротора ω не может быть равной скорости вращения поля, так как при этом не
будет индуцироваться вторичная ЭДС e2, что приведет к отсутствию
вращающегося момента. Поэтому ротор в своем движении должен отставать от
магнитного поля - проскальзывать - отсюда наименование двигателя - асинхронный,
а один из основных параметров - скольжение:
Часто рассматривают
так называемую однопериодную модель двигателя, в которой p=1,
тогда
Скольжение является
относительной величиной и в двигательном режиме изменяется в пределах 0<S≤1,
причем S=0 соответствует синхронной работе, а S=1- пуску двигателя.
Частота
индуцируемых во вторичной обмотке (роторе) ЭДС и токов зависит от скольжения
Тогда эквивалентную
схему цепи ротора можно представить согласно .
.
Рис. 3-2а. Эквивалентная схема цепи ротора асинхронной машины.
В начальный момент
пуска двигателя ротор неподвижен S=1, ω2=
ω1, и в роторе индуцируется ЭДС, пропорциональная первичной
частоте
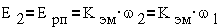
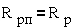
В рабочем режиме
ω2<ω1, так как S<1
Эквивалентная схема
цепи ротора в рабочем режиме показана на 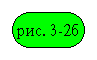 . Она содержит изменяемый источник ЭДС Eрп·S и изменяемое индуктивное
сопротивление xр=xрп·S.
. Она содержит изменяемый источник ЭДС Eрп·S и изменяемое индуктивное
сопротивление xр=xрп·S.
Рис. 3-2б. Эквивалентная схема цепи ротора асинхронной машины.
Пользуясь этой
схемой можно вычислить ток ротора
Разделив это выражение
на S, получим
Пользуясь формулой (3-3)
получим эквивалентную схему цепи ротора, приведенную к параметрам пускового
режима, то есть при неподвижном роторе (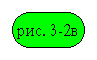 ).
).
Рис. 3-2в. Эквивалентная схема цепи ротора асинхронной машины.
В этой схеме ЭДС
ротора и его индуктивное сопротивление не изменяется при изменении скольжения
(частоты вращения), а изменяется активное сопротивление, хотя физически
происходит все наоборот - при изменении частоты вращения изменяется частота
вторичной ЭДС f2 и из-за этого меняется ее амплитуда и индуктивное
сопротивление цепи ротора.
Приведя рабочий
режим двигателя к режиму неподвижного ротора, можем рассматривать асинхронную
машину как обычный трансформатор с неподвижными обмотками, схема которого
показана на 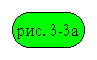 , где n- коэффициент трансформации.
, где n- коэффициент трансформации.
Рис. 3-3а. Эквивалентная электрическая схема асинхронного двигателя.
Приведя параметры вторичной
цепи и первичной, получим окончательную эквивалентную схему асинхронного
двигателя, показанную на 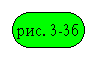 ,
,
Рис. 3-3б. Эквивалентная электрическая схема асинхронного двигателя.
где 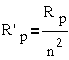
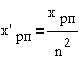
На основании этой
схемы получим выражение для тока ротора
Выражение для
вращающегося момента можем получить из энергетического уравнения M·ω1= M·ω+m1·Ip2·Rp, где m1- количество фаз.
Левая часть
уравнения - электромагнитная мощность, а правая - механическая плюс
электрическая мощности.
Из этого уравнения
получим:
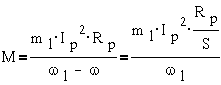
Подставляя сюда
выражения для тока ротора 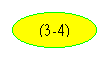 и
учитывая, что
и
учитывая, что 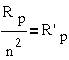
График зависимости электромагнитного
момента от скольжения представлен на  .
.
Рис. 3-4а. Зависимость электромагнитного момента от скольжения.
Правая часть
графика относится к режиму двигателя, а левая - генератора. Скольжение,
соответствующее максимальному моменту, называется критическим и обозначается SK или SM. Выражение для момента двигателя может быть представлено через
параметры критической точки
где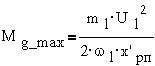
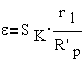
При пренебрежении
активным сопротивлением статора r1=0, ε=0, получим более
простое выражение для момента
Критическое
скольжение за зависит от соотношение активного и индуктивного сопротивлений
ротора. При r1=0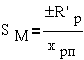
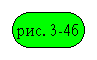 .
.
Рис. 3-4б. Зависимость электромагнитного момента от скольжения.
Характеристика 1
соответствует случаю R`p<xрп, а характеристика 2 - R`p>xрп, т.е. в зависимости от
величины активного сопротивления ротора критическое скольжение может быть как меньше,
так и больше единицы. В трехфазных двигателях SM<1, а в двухфазных SM>1.
В ряде случаев в
двухфазных и однофазных асинхронных двигателях производится питание
несимметричным напряжением, что приводит к появлению пульсирующего магнитного
поля. По принципу суперпозиции несимметричную систему можно представить в виде
двух симметричных, но создающих магнитные поля, вращающиеся в противоположных
направлениях, прямом и обратном. Суммарный вращающий момент будет равен
алгебраической сумме двух моментов - прямого и обратного, выражения для которых
аналогичны 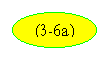
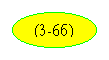 .
.
При пренебрежении
активным сопротивлением статора это выражение будет иметь вид:
Характеристики при
несимметричном питании показаны на  .
.
Рис. 3-5. Характеристики асинхронного двигателя при несимметричном питании.
а) Mmax_пр>Mmax_обр
б) Mmax_пр=Mmax_обр
На  Mmax_пр>Mmax_обр
и существует пусковой момент Mп, который можно изменять,
меняя несимметрию питающих напряжений, как это делается в управляемых асинхронных
двухфазных двигателях. На
Mmax_пр>Mmax_обр
и существует пусковой момент Mп, который можно изменять,
меняя несимметрию питающих напряжений, как это делается в управляемых асинхронных
двухфазных двигателях. На  Mmax_пр=Mmax_обр
и пусковой момент равен нулю, как это бывает в однофазных двигателях. Но если
двухфазный двигатель с помощью дополнительной обмотки, как это обычно делается,
то при S<1 появляется вращающий момент и двигатель будет вращаться, находясь
в рабочей точке Sном, Mном.
Mmax_пр=Mmax_обр
и пусковой момент равен нулю, как это бывает в однофазных двигателях. Но если
двухфазный двигатель с помощью дополнительной обмотки, как это обычно делается,
то при S<1 появляется вращающий момент и двигатель будет вращаться, находясь
в рабочей точке Sном, Mном.
3.2. Асинхронные трехфазные
двигатели
В асинхронном
трехфазном двигателе вращающееся магнитное поле создается тремя обмотками
статора, на которые подается трехфазное напряжение сети.
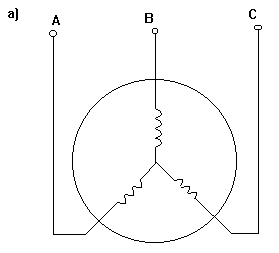
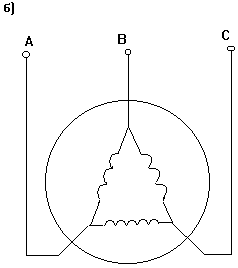
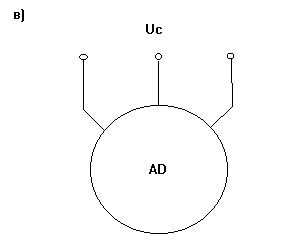
Схема трехфазного
двигателя и временная диаграмма питающего напряжения показаны на  .
.
Рис. 3-6а,б,в. Схемы включения асинхронного двигателя.
Рис. 3-6г. Временная диаграмма питающих напряжений асинхронного двигателя.
Для двигателей
основной является механическая характеристика ω=f(M), то есть зависимость
частоты вращения от момента, которая для асинхронного двигателя может быть
получена на основании выражения  или
или
 с учетом связи
между скольжением S и частотой вращения ω. Вид механической
характеристики показан на
с учетом связи
между скольжением S и частотой вращения ω. Вид механической
характеристики показан на  .
.
Рис. 3-7а. Механическая характеристика асинхронного трехфазного двигателя.
Ее можно разбить на
два участка - рабочий (0-а) при 0<S<SM и участок пуска (a-b) при SM<S<1. Обычно в асинхронных трехфазных двигателях с
короткозамкнутым ротором SM=0.05..0.15, т.е.
характеристики достаточно жесткие и рабочая частота вращения ωн
близка к синхронной ω0. Для таких двигателей на рабочем участке
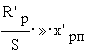
 сопротивлениями
x´рп и r1 по сравнению с
сопротивлениями
x´рп и r1 по сравнению с 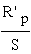
откуда
где ω -
частота вращения ротора, ω1- частота вращения поля, Uc- напряжение питания сети, R´p-
приведенное сопротивление ротора. Как видно из выражения  и
и  , изменение напряжения питания мало влияет на
частоту вращения ротора на рабочем участке и диапазон управления напряжением
весьма ограничен.
, изменение напряжения питания мало влияет на
частоту вращения ротора на рабочем участке и диапазон управления напряжением
весьма ограничен.
Рис. 3-7б. Механическая характеристика асинхронного трехфазного двигателя.
Несколько больший
диапазон может быть обеспечен двигателем повышенного скольжения (SM≥1). Однако в этом случае механические характеристики имеют
большую крутизну ( ) и устойчивая работа двигателя может быть
достигнута лишь при использовании замкнутой системы, обеспечивающей
стабилизацию скорости. При изменении статического момента система регулирования
поддерживает заданный уровень скорости и происходит переход с одной
механической характеристики на другую, в итоге работа протекает на характеристиках,
показанных на
) и устойчивая работа двигателя может быть
достигнута лишь при использовании замкнутой системы, обеспечивающей
стабилизацию скорости. При изменении статического момента система регулирования
поддерживает заданный уровень скорости и происходит переход с одной
механической характеристики на другую, в итоге работа протекает на характеристиках,
показанных на  штриховыми линиями.
штриховыми линиями.
Рис. 3-7в. Механическая характеристика асинхронного трехфазного двигателя.
Плавное
регулирование скорости в широких пределах с сохранением достаточной жесткости
характеристик возможно только при частотном управлении. Как видно из формулы  , изменяя частоту
вращения поля ω1, можно изменять частоту вращения ротора ω
за счет первого слагаемого формулы, при этом желательно, чтобы второе слагаемое
не менялось, т.е. жесткость характеристики при этом не изменялась. Для этого
одновременно с частотой, изменяют напряжение питания Uc так, чтобы их отношение
оставалось постоянным
, изменяя частоту
вращения поля ω1, можно изменять частоту вращения ротора ω
за счет первого слагаемого формулы, при этом желательно, чтобы второе слагаемое
не менялось, т.е. жесткость характеристики при этом не изменялась. Для этого
одновременно с частотой, изменяют напряжение питания Uc так, чтобы их отношение
оставалось постоянным 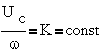
Тогда рабочий
участок механической характеристики при частотном управлении можно приближенно
представить формулой:
Такое управление
называется пропорциональным частотным управлением.
Вид механических
характеристик при пропорциональном управлении показан на  .
.
Рис. 3-8а. Частотное управление асинхронным двигателем.
Функциональная схема
частотного управления представлена на  .
Она состоит из управляемого выпрямителя УВ, преобразующего сетевое напряжение
переменного тока частотой 50 Гц в напряжение питания постоянного тока Uп, величина которого может
регулироваться от устройства управления УУ, и автономного инвертора АИ,
преобразующего напряжение Uп в трехфазное напряжение
изменяемой частоты f1. Управляющее устройство, изменяя частоту f1в в зависимости от задания
ωз, изменяет также и напряжение Uп так, чтобы их отношение
оставалось постоянным. Система управления может иметь обратную связь по
скорости вращения через тахогенератор ТГ.
.
Она состоит из управляемого выпрямителя УВ, преобразующего сетевое напряжение
переменного тока частотой 50 Гц в напряжение питания постоянного тока Uп, величина которого может
регулироваться от устройства управления УУ, и автономного инвертора АИ,
преобразующего напряжение Uп в трехфазное напряжение
изменяемой частоты f1. Управляющее устройство, изменяя частоту f1в в зависимости от задания
ωз, изменяет также и напряжение Uп так, чтобы их отношение
оставалось постоянным. Система управления может иметь обратную связь по
скорости вращения через тахогенератор ТГ.
Рис. 3-8б. Функциональная схема частотного управления.
Более совершенным,
чем пропорциональное управление, является частотно-токовое управление, при
котором контролируется, кроме частоты вращения, ток якоря от датчика тока (ДТ),
как показано на  ,
что позволяет оставлять постоянным поток при изменении частоты f1 и нагрузки.
,
что позволяет оставлять постоянным поток при изменении частоты f1 и нагрузки.
Как динамическая
система асинхронный трехфазный двигатель описывается нелинейным
дифференциальным уравнением первого порядка:
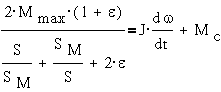
где J-
момент инерции ротора.
Учитывая, что
ω=ω0·(1-S) и 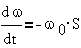
Учитывая, что 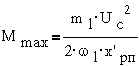
Этому уравнению
соответствует структурная схема, представленная на  .
.
Рис. 3-9а. Структурная схема асинхронного трехфазного двигателя.
Интегрируя
уравнение ( ) в пределах от S1 до S, получим
) в пределах от S1 до S, получим
где 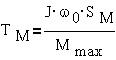
Выражение ( ) позволяет
построит кривые переходного процесса S=f(t) и соответственно ω=f(t),
вычисляя ряд значений t при неизменном S1 и изменяющемся S.
Кривые разгона двигателя при различных SM приведены на
) позволяет
построит кривые переходного процесса S=f(t) и соответственно ω=f(t),
вычисляя ряд значений t при неизменном S1 и изменяющемся S.
Кривые разгона двигателя при различных SM приведены на  . Как видно,
длительность переходного процесса существенно зависит от SM и при
некотором значении SM_опт минимальна. Двигатели
повышенного скольжения являются более быстродействующими, так как SM_опт≈0.4..0.5.
. Как видно,
длительность переходного процесса существенно зависит от SM и при
некотором значении SM_опт минимальна. Двигатели
повышенного скольжения являются более быстродействующими, так как SM_опт≈0.4..0.5.
При
пропорциональном частотном управлении для малых приращений двигатель можно
описать линейными уравнениями (см. 3-1)
Этим уравнениям
соответствует структурная схема, представленная на  .
.
Рис. 3-9в. Структурная схема асинхронного трехфазного двигателя.
На основании
анализа этой схемы можно получить передаточную функцию двигателя при частотном
управлении
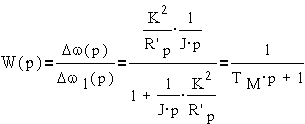
где K -
электромеханическая постоянная времени.
3.3. Асинхронные двухфазные
управляемые двигатели
Трудности
управления трехфазными двигателями привели к использованию в приводах малой
мощности управляемых двухфазных двигателей, имеющих две обмотки - обмотку
возбуждения и обмотку управления, напряжения в которых сдвинуты на 90o электрических
градусов, как показано на  и
и
 .
.
Рис. 3-10а. Схема асинхронного двухфазного двигателя.
Рис. 3-10б. Временные диаграммы питания асинхронного двухфазного двигателя.
Для упрощения
управления осуществляется управление воздействием только на одну обмотку -
обмотку управления через усилительно преобразующее устройство - УПУ. Вторая
обмотка через конденсатор подключается к сети.
При регулировании
тока в обмотке управления по величине и фазе вносится асимметрия в МДС обмоток,
и вместо кругового магнитного поля в машине возникает электрическое поле. При
этом наряду с напряжениями и токами прямой последовательности фаз, создающими
двигательный режим, возникает напряжение и токи обратной последовательности,
вызывающие торможение. Таким образом, меняя степень асимметрии, можно
регулировать скорость двигателя.
В зависимости от
того, как создается в машине асимметрия магнитного поля, различают три способа
управления: амплитудный, фазовый и амплитудно-фазовый.
Чаще всего
используется амплитудное несимметричное управление, когда UB=UC, а Uγ=α·Uc, где α меняется
от 0 до 1. Пользуясь соотношениями  и
и
 можно получить
выражения для вращающего момента при амплитудном управлении:
можно получить
выражения для вращающего момента при амплитудном управлении:
При симметрии
напряжений, когда α=1, из уравнения 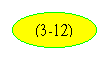 получим
нормальное уравнение - выражение для асинхронной машины
получим
нормальное уравнение - выражение для асинхронной машины 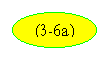 .
.
Так как в
двухфазных двигателях SM>1, то при α=0,
т.е. при отключении обмотки управления двигатель тормозится, так как второе
слагаемое в 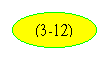 становится больше
первого и останавливается при S=1, когда оба слагаемых
становятся одинаковыми.
становится больше
первого и останавливается при S=1, когда оба слагаемых
становятся одинаковыми.
Механические
характеристики при амплитудном управлении для случая SM=2 и ε=3 приведены на  слева.
слева.
Рис. 3-10в. Статические характеристики асинхронного двухфазного двигателя.
Пусковой момент
можно получить из уравнения 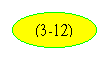 ,
положив S=1.
,
положив S=1.
На  справа показаны
регулировочные характеристики, которые могут быть получены непосредственно из
механических.
справа показаны
регулировочные характеристики, которые могут быть получены непосредственно из
механических.
Эти характеристики
могут быть линеаризованы, и асинхронный двигатель представлен как линейная динамическая
система, описываемая следующими уравнениями:
где KU и Kω- коэффициенты передачи, получаемые при линеаризации характеристик, как
показано на  .
.
Рис. 3-11а. Линеаризация характеристик АДД.
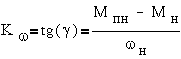
Уравнениям 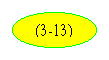 соответствует
структурная схема , представленная на
соответствует
структурная схема , представленная на 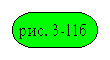 .
.
Рис. 3-11б. Структурная схема АДД.
По этой схеме можно
получить передаточную функцию АДД
где 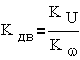
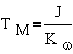
3.4. Упражнения и контрольные
вопросы к главе 3.